Yellow Sapphire: Natural, Heat-Treated, Beryllium-Diffused, and Synthetic

John L. Emmett, Ungkhana Atikarnsakul, Jennifer Stone-Sundberg, and Supharart Sangsawong

ABSTRACT

Natural yellow sapphires are colored by one of two entirely different chromophores or by a combination of the two. These two chromophores are iron (Fe³⁺) and a trapped hole paired with iron (h^•-Fe³⁺). The color saturation of the Fe³⁺ chromophore, as previously documented, does not linearly depend on its areal density, unlike the other five chromophores in natural corundum. It exhibits a complex dependence on areal density, a relationship that is explored here. Low-iron-content natural yellow sapphires are colored solely by the h^•-Fe³⁺ chromophore. The yellow sapphires from Sri Lanka are colored in this way. Some of the basalt-hosted high-iron sapphires from Australia and Thailand are colored by h^•-Fe³⁺ in addition to Fe³⁺. Natural sapphires that are colorless or weakly yellow often develop strong yellow coloration via heat treatment. They depend on formation of the h^•-Fe³⁺ chromophore for that change. In these natural stones that respond to heat treatment, one of two different internal chemistries is present, which must be altered to bring about the color enhancement. These two chemistries, which require two different heat treatment processes, are presented. The diffusion of beryllium into various types of sapphire can shift their chemistry from donor- to acceptor-dominated, forming the trapped hole, h^•, which pairs with iron to produce the intense yellow coloration. Although crystals with the h^•-Fe³⁺ chromophore were grown as a part of our study, synthetic yellow sapphires are not often colored by the same chromophores of natural sapphires. They are usually colored by the Ni³⁺ chromophore or by Ni³⁺ and Cr³⁺. Somewhat surprisingly, the color saturation of Czochralski-grown nickel-doped sapphire can sometimes be enhanced by heat treatment.

The complexities of yellow sapphire have been discussed in some detail for many years (e.g., Schmetzer et al., 1983; Nassau and Valente, 1987). A clear understanding of the nature of the multiple types of yellow sapphire was inhibited by the lack of understanding of the individual chromophores and their individual absorption spectra. The chromophores that cause yellow color in natural corundum have been recently elucidated (Emmett et al., 2017a; Dubinsky et al., 2020), allowing the more detailed study of yellow sapphire and its heat treatment, presented here. This work intends to provide a clear basis for future study of yellow sapphire and its individual color stabilities.

Yellow sapphires are found in a wide range of deposits worldwide. They are colored by two entirely different chromophores: the iron (Fe³⁺) chromophore and the trapped hole paired with iron (h^•-Fe³⁺)¹ (figure 1). These two chromophores represent the two extremes of natural chromophore strength in corundum. In faceted stones up to several carats, a few thousand ppma of Fe³⁺ are required for good coloration, while only a few ppma of h^•-Fe³⁺ produce similar levels of color saturation (Dubinsky et al., 2020). It is not unusual for high-iron yellow sapphires from basalt-hosted deposits to be colored by both chromophores. In the past, the combination of these two chromophores in the same stone at dramatically different concentrations has impeded a complete understanding of the cause of color.

The h^•-Fe³⁺ chromophore arises in natural stones that are acceptor dominated, meaning the divalent cation concentration exceeds the sum of the tetravalent cation concentration and the excess divalent cation concentration is not charge compensated by H⁺ or oxygen vacancies. Because heating in an oxygen atmosphere can diffuse hydrogen out of the stone or oxidize the oxygen vacancies, colorless or weakly yellow stones can often be heat treated to create rich yellow gems.

The total amount of iron in natural corundum ranges from a few ppma to nearly 5000 ppma. Iron in natural corundum can exist in two valence states: Fe²⁺ and Fe³⁺. The cation site in corundum is trivalent (Al³⁺). When iron alone occupies this site, it will be primarily trivalent. For Fe²⁺ to exist in natural corundum, it must be charge compensated by a donor such as Si⁴⁺, Ti⁴⁺, H⁺, or one-half of an oxygen vacancy, as the crystal must remain electrically neutral. Oxygen vacancies and H⁺ only exist in natural corundum at low concentrations (a few ppma). Thus, any significant amount of Fe²⁺ can only exist if it is paired with Ti⁴⁺ or Si⁴⁺. Concentrations of Ti⁴⁺ and Si⁴⁺ rarely exceed a few hundred ppma in natural corundum, and it is unclear how much of that is actually in solution in the lattice. Some portion of the Si⁴⁺ and Ti⁴⁺ will also have to preferentially charge compensate Mg²⁺ if present, as its level lies below that of Fe²⁺ in the band gap. Only Fe²⁺ charge compensated by H⁺ ions or by oxygen vacancies would be expected to exhibit an Fe²⁺ spectrum. Such spectra are expected to be in the near-infrared region and be very weak. If charge compensated by Ti⁴⁺ or Si⁴⁺, extremely strong pair spectra will result (e.g., the Fe²⁺-Ti⁴⁺ pair resulting in the blue color of sapphire).

¹The symbol h^• is the symbol for an electron hole in Kröger-Vink notation, and h^•-Fe³⁺ means that the hole has paired with an Fe³⁺ ion. See box B.

MATERIALS AND METHODS

The corundum samples in this study represent many different deposits around the world and were chosen from the Crystal Chemistry collection and GIA’s colored stone reference collection in Bangkok. Samples with three- and four-digit designations are from the Crystal Chemistry collection, while those with nine- to twelve-digit designations are from GIA’s colored stone reference collection. Samples used to characterize the Fe³⁺ and h^•-Fe³⁺ chromophores originated from Myanmar, Thailand, Cambodia, Sri Lanka, Australia, Nigeria, Cameroon, Rwanda, Nigeria, Kenya, and the United States (Montana). Additionally, several synthetic crystals were grown using the Czochralski method by Saint-Gobain Crystals and Detectors and by Teledyne FLIR Scientific Materials. A yellow synthetic nickel-doped sapphire grown using the Verneuil method was purchased from RusGems in Bangkok. All wafer samples were crystallographically oriented using a crystal alignment instrument with the c-axis either perpendicular or parallel to the plane of the wafer (Thomas et al., 2014). Trace element concentrations were determined either by laser ablation–inductively coupled plasma–mass spectrometry (LA-ICP-MS) using the current standards at GIA in Bangkok (Stone-Sundberg et al., 2017), by secondary ion mass spectrometry (SIMS) against ion implant standards at Caltech (Stone-Sundberg et al., 2020), or by both. In addition, ultraviolet/visible/near-infrared (UV-Vis-NIR) spectra of 102 of these wafer samples were measured, from which 24 were chosen for this study of the 450 nm Fe³⁺ band, as they represent equal concentration intervals of iron from most to least concentrated. Because the trace element concentrations in natural sapphires are often not uniform, the 24 samples used for the study of the Fe³⁺ chromophore were measured at four points on each side of the sample within the optical aperture of the sample plate. We required that the standard deviation of these eight data points be less than 6%. These sample selection criteria greatly minimized spatial concentration variations. The iron concentration in these samples covered the 56.5–4730 ppma region. The 450 nm Fe³⁺ absorption cross section² was too weak to accurately fit the curve below this lower value.

²The terms absorbance, absorption coefficient, absorption cross section, ion density, and areal defect density are defined in box A.

In addition, large samples (25–50 g each) of rough stones in the 3.5–7.0 mm range were used for many individual heat treatment experiments to test for acceptor domination before spectroscopic samples were chosen for these types of material. These stones were from the Rock Creek, Dry Cottonwood Creek, and Eldorado Bar deposits in Montana; Sri Lanka; the Chimwadzulu Hill deposit in Malawi; several Madagascar deposits; the Kings Plain deposit in New South Wales, Australia; and the Songea deposit in Tanzania.

Optical absorption measurements were obtained with Hitachi 2900 and 2910 spectrophotometers at Crystal Chemistry and with a Hitachi 2910 at GIA in Bangkok. The Hitachi 2910 units were reengineered by Tim Thomas (Applied Materials, Portland, Oregon) to have a rotatable polarized optical beam so that both E⟂c and Ellc spectra could be measured on wafers with the c-axis in the plane of the wafer. These instruments measure the spectra to a resolution of 1.5 nm. The optical absorption data was corrected for the multiple reflections between the two optical surfaces of the sample wafers (see box A).

BOX A: PRESENTING DATA

It is perhaps unfortunate, but like many other measurements that have been devised, there are multiple sets of units used to quantify the optical absorption features of gemstones, minerals, and other materials.   Figure A-1. Illustration of incident light being transmitted through a sample of a given thickness. Assuming zero reflection losses from the two sample surfaces in figure A-1, the Beer-Lambert law can be expressed using several different units:   Where: I0 = incident light intensity I = transmitted light intensity T = transmission in percent A = decadic true absorbance as measured by the spectrophotometer (a unitless ratio) a = decadic absorption coefficient in cm–1 d = sample thickness in cm ε = molar absorptivity in liter mole–1 cm–1, also called the extinction coefficient c = chromophore concentration in moles per liter α = naperian true absorption coefficient in cm–1 C = chromophore concentration in absorbers per cm3 σ = true absorption cross section in cm2 e = base of the natural logarithm = 2.71828… Absorbance Current commercial spectroscopic instruments measure the absorbance, A, in decadic units defined as:   Thus, data presented in the literature in units of A are unambiguous. Absorption Coefficient Two different absorption coefficients are currently present in the literature. As a very general statement, physicists and materials scientists studying the absorption strength of ions in crystals and glasses tend to use:   This is the set of units we have used in this article and in Emmett et al. (2017a) and Dubinsky et al. (2020). It is also the system of units used in GIA’s colored stone reference collection database. Chemists and mineralogists (e.g., Rossman, 1988) have generally expressed absorption coefficient as:   These two representations are very simply related by:   While we have used a and α to clearly show the difference, α is often used in the literature for either absorption coefficient. With the rise of multidisciplinary sciences and the rapid spread of materials science, the usage has become very mixed. In fact, one can often find both conventions in papers presented at the same technical meeting. It is important to note that just because the term absorption coefficient is used with the symbol α, it is not clear which system is in use unless the simple equation is stated. Therefore, it is very important for scientists to present the simple equation that defines their units in both published papers and presentations. Absorption Cross Section and Extinction Coefficient Now suppose we were to compare different chromophores in corundum, or the same chromophore in different hosts, in terms of their absorption strength and the depth of color they produce. If we divide the absorption coefficient by the concentration, C, of the chromophore, we can define an absorption cross section spectrum, σ, which is independent of concentration or sample thickness, as shown in equation A-1. The absorption cross section is calculated from α or A as:   The absorption cross section spectrum depends only on the characteristics of an individual chromophore ion (e.g., Cr3+) and the particular host (i.e., corundum), and it is measured in square centimeters (cm2). The unit of square centimeters denotes an area, and one can think of the cross section as the “area” of an individual ion as seen by the photons in a light beam. However, it does not represent the physical size of the ion. This absorption cross section is used for comparisons in this article and in Dubinsky et al. (2020). In chemistry and mineralogy, epsilon (ε) is often used for the extinction coefficient, which is the same concept but in a different set of units. From equation A-1, we have:   As shown above, the units of ε are liter mole–1 cm–1. The extinction coefficient for corundum is easily calculated from σ by the following from equation A-1:   Thus:     Figure A-2. UV-Vis-NIR plot of both the absorption cross section and the extinction coefficient for oriented spectra of Cr3+:Al2O3. Figure A-2 compares the numerical values of the extinction coefficient and the absorption cross section for the Cr3+ ion in corundum. The term extinction coefficient is also called the molar absorptivity in some publications, but the units are the same. Units Used on Plots A variety of descriptions are used on spectra plots when the axis values are far larger or smaller than can be easily represented without exponents. In figure A-2, the values plotted on the vertical axis range from 0 to 4 × 10–19 cm2. There are several ways in which these units have been represented in the literature: 1. Absorption Cross Section × 1019 cm2 2. Absorption Cross Section in units of 10–19 cm2 3. Absorption Cross Section × 10–19 cm2 In previous publications we have used unit 1, which is quantitatively correct but confusing to readers unfamiliar with exponential notation (Emmett et al., 2017a; Dubinsky et al., 2020). Unit 2 is probably the clearest and simplest but takes up more space on the graph. Unit 3 is very common in the scientific literature, but it is formally incorrect since the numbers shown on the plot are 0 to 4. As unit 2 is the clearest, we have chosen to use it instead of unit 1 in this article with the hope of eliminating ambiguity. Concentration Units Generally, there are two major ion concentration units in the literature: ions/cm3 and moles/liter. The literature often uses ppma, which is ions/cm3 divided by 106 (1 ppma in corundum is 1.178 × 1017 ions/cm3). Moles/liter is easily converted to ions/cm3. One mole/liter equals Avogadro’s number divided by 1000 cm3, or 6.0221 × 1020 ions/cm3. For corundum, 1 mole/liter equals 5111 ppma. Areal Density The areal density (ρA) is simply the product of the ion concentration, in ions/cm3 times the sample thickness, d, in cm. Thus, the units are ions/cm2. Under the color circles in this paper, we present the areal density in ppma-cm. This factor is:   where 1.178 × 1017 is the number of ions in 1 cubic centimeter of Al2O3 determined by:   where A is Avogadro’s number (6.022 × 1023 molecules/mole), ρ is the density of corundum (taken as 3.99 grams/cm3), and M is the molecular weight of corundum (101.961 grams/mole). Correction for Surface Reflection Losses To determine the true absorbance A as defined in equation A-1 above, the instrument-measured absorbance, must first be corrected for the loss from multiple reflections between the two polished surfaces of the sample. This is done by summing all the reflections between the two surfaces (T.S. Hemphill, pers. comm., 2011) and using a three-term Sellmeier equation for corundum to determine the sample’s refractive index as a function of wavelength (Tatian, 1984). The index input data to the Sellmeier equation is a combination of all relatively recent data from the suppliers of high-purity synthetic corundum material used to fabricate high-purity optical elements. The Sellmeier equation fit to these data was performed for us by John Trenholme (formerly with Lawrence Livermore National Laboratory) using TableCurve 2D software. Correcting for this loss, we have the true absorbance, A. This correction is important because it is greatest where the absorption is least, and it is just this region of the absorption spectrum that transmits the most intense light and thus contributes most to the color. This reflection correction has been made for all spectra presented in this article and for all spectra used in deriving these results. It is also important to remember that very strong absorption peaks, if very narrow, will have little impact on color. Since commercial instrumentation is now available to measure the refractive index of flat samples at multiple wavelengths, it is suggested that these technologies be acquired by major gemological laboratories to add to their databases and to provide for correction of optical spectra of other gem minerals.

Fourier-transform infrared (FTIR) spectra were measured using Thermo Nicolet 6700 and iS50 FTIR spectrometers operating with a Pike 4× beam condenser accessory at a resolution of 2 cm^–1. The FTIR spectrometer was also connected to an air compressor with a purge gas generator (Parker Balston model 75-52) to minimize water and carbon dioxide contamination of the sample and the air in the sample chamber, as these compounds absorb light and obscure spectral peaks of interest. This helps to minimize moisture and carbon dioxide features, improve signal-to-noise ratio, and achieve a flat baseline. Spectra were collected from each sample through a hole of size chosen to accommodate a particular sample in the aluminum sample plate from the same location where the optical absorption spectra were collected.

The low-temperature heat treatment experiments of wafer samples in air were conducted at GIA in Bangkok using a Thermolyne FB1400 benchtop 1100°C muffle furnace manufactured by Thermo Scientific. The high-temperature (>1100°C) experiments in controlled atmospheres were conducted by Crystal Chemistry and by Columbia Gem House (Vancouver, Washington) with modified Thermal Technology 1000A graphite furnaces, using Coors Tek 998 alumina muffle tubes to allow the use of carefully controlled atmospheres.

The beryllium diffusion experiments were conducted at Crystal Chemistry in the Thermal Technology furnace described above. Diffusion experiments were run at 1780° or 1800°C in pure oxygen for 33 hours. This procedure is discussed at length in Emmett et al. (2003).

Color coordinates (Berns, 2000) were calculated from the sample’s transmission spectrum and the characteristics of the light source. Calculations of the color coordinates for a given color temperature were performed via Thermo Scientific’s GRAMS/AI spectroscopy software, a general-purpose spectra manipulation code that includes color coordinate calculations. Among the many color coordinate systems, the CIE 1976 L*a*b* system was chosen for its approximately uniform color space, and we selected a color temperature of 5000K.

RESULTS

The Fe³⁺ Chromophore. Fe³⁺ exists in essentially all natural sapphire. The resulting stones can be colorless, yellow, green, or blue, depending on the relative concentrations of the various trace elements present. This study examined 102 samples, from which 24 of the 102 data sets were chosen to represent the entire set based upon their evenly spaced representation of the iron concentrations for the 102 samples. Yellow sapphires colored primarily by iron are often found in basalt-hosted blue sapphire deposits. A single crystal will often contain both deep blue and deep yellow regions in varying proportions. Although bicolor stones are occasionally faceted, these will usually be cut as either blue or yellow gems, depending on the predominant color. Several of the high-iron samples from this study were bicolor stones containing well-defined blue and yellow regions. These samples were fabricated with their planes either perpendicular or parallel to the c-axis, depending on which orientation most clearly separated the blue and yellow regions. Figure 2 shows a selection of yellow wafers for spectroscopy. Figure 3 shows a selection of the bicolor wafers.

Often in the study of corundum chromophores, an effective procedure has been to grow a crystal containing only one chromophore. However, that procedure was not successful for Fe³⁺ because of decomposition and vaporization of the iron oxides at the Czochralski growth temperature. Thus, 23 of the 24 natural samples chosen for this study were selected from a wide range of deposits worldwide.

Figure 4 shows both the E⟂c and Ellc absorption spectra of sample 1245, from the Garba Tula deposit in Kenya. This sample contains 3126 ppma iron. There are three absorption bands from Fe³⁺ and Fe³⁺ pairs in the visible region of the spectrum (Ferguson and Fielding, 1971, 1972; Krebs and Maisch, 1971) at 450, 530, and 700 nm. Of these, the 450 nm band is by far the dominant cause of color. Because it absorbs in the blue region of the spectrum, the transmitted color is yellow. The 530 and 700 nm bands are broad and very weak. Taken together, this combination has little impact on color. The 450 nm Ellc band is nearly identical to the E⟂c band, but the peak amplitude is about 16% less. Thus, we have focused our study of the iron chromophore on the 450 nm E⟂c band.

In the course of previous work on the Fe³⁺ chromophore (Dubinsky et al., 2020), two unique features were observed with the 450 nm absorption band, which is the primary determinant of color. First, the peak absorption cross section increases with iron concentration; second, the full width at half maximum (FWHM) of the band increases by about a factor of two from the lowest to the highest iron concentrations (figure 5; see also figure 7 of Dubinsky et al., 2020). Such increases in both peak absorption cross section and width of the 450 nm absorption band more than linearly increase the strength of the chromophore with concentration. Other chromophores in natural corundum do not show these changes and thus exhibit a constant strength with concentration.

The concentration of Fe³⁺ in natural corundum ranges from <5 ppma to at least 4730 ppma. Since the 450 nm Fe³⁺ absorption cross section is low (~10^–20 cm²), optical measurements were limited to samples whose concentration was above 50 ppma. For example, the peak absorption coefficient at 450 nm of sample 1272 with 79.2 ppma and a thickness of 3.415 mm is 0.042 cm^–1. The peak absorbance as measured by the spectrophotometer is therefore 0.0062. At 10–20% of this peak value we see instrumental noise problems. Thus, spectrophotometer noise and sample thickness determined the minimum concentration used. Therefore, for this study we were limited to using samples with Fe³⁺ concentrations that ranged from 56.5 to 4730 ppma.

Of the samples used for this study, 24 were chosen, covering the range from 56.5 to 4730 ppma iron for the iron chromophore data presented here. The E⟂c spectra of these samples were accurately curve fit to make the best determination of the 450 nm band magnitude and shape. Curve fitting was performed with GRAMS/AI (Thermo Scientific) using a linear baseline plus four Lorentzian bands (as suggested by Dr. Ren Lu of the Gemmological Institute, China University of Geosciences in Wuhan). The usual variety of other band shapes were evaluated for the quality of the fit, and the Lorentzian bands produced the best match for four bands or fewer.

Determining the baseline for the 450 nm E⟂c band presented some difficulty, as it was overlapped to some degree by the 388 nm Fe³⁺ band and by the 580 nm E⟂c Fe²⁺-Ti⁴⁺ band in the blue sapphires. Because these interferences vary widely in magnitude throughout the large number of samples used, it was necessary to modify the spectra of some of the deep blue sapphire samples so that the 450 nm band did not fall on a steeply rising portion of the Fe²⁺-Ti⁴⁺ band. The modification was achieved by subtracting successively larger portions of an Fe²⁺-Ti⁴⁺ spectrum from the sample spectrum until the minima on either side of the 450 nm peak were of the same amplitude. The spectrum used for this subtraction is the absorption cross section determined for the Fe²⁺-Ti⁴⁺ pair (Dubinsky et al., 2020), multiplied by appropriate concentrations.

Even though the 450 nm band is quite narrow, the use of a linear baseline creates some error because the background decreases toward the 450 nm peak from longer wavelengths and shorter wavelengths. This error is estimated as ≤10% of the peak amplitude. A typical curve fit is shown in figure 6 for a sample containing 447 ppma iron. Note the typical quality of the fit by comparing the experimental data final baseline with the fitted peak baselined in figure 6.

Figure 7A shows the 450 nm Fe³⁺ band peak absorption cross section data as a function of iron concentration of the 24 curve-fit samples.

From this plot, we can see that the absorption cross section is essentially constant as the iron concentration increases from low values up to ~700 ppma. Above 700 ppma, it increases to a value at 4730 ppma iron, which is about 4.5 times the low concentration value. The slope of the curve over the region from 900 to 4730 ppma iron is approximated by the proportionality given in equation 1, where σ is the absorption cross section:

In figure 7A, the lowest concentration measured was of a synthetic iron-doped crystal grown by Saint-Gobain Crystals and Detectors. The cross section of this sample (shown in red) is noticeably smaller than that of the three natural samples containing less than 100 ppma iron. This may imply that the clustering of iron in corundum is dependent on the thermal history of the sample.

The data of figure 7A could also be presented as the 450 nm peak absorption coefficient versus the Fe³⁺ concentration. This allows an estimate of the Fe³⁺ concentration if the peak absorption coefficient has been measured, or vice versa. The plotting of data in this fashion is shown in figure 7B.

As indicated earlier, in addition to the absorption cross section increase with concentration, the FWHM of the 450 nm peak also increases substantially with concentration. The strength of the Fe³⁺ chromophore is determined by both the peak absorption cross section and the FWHM of the 450 nm band. Figure 8 compares the curve shape of the lowest- and highest-concentration samples. The peak value of each spectrum is normalized to 1.0.

As shown in figure 8, the peak of the low-Fe³⁺ sample is at 449.5 nm while that of the high-Fe³⁺ sample is at 451.5 nm, a shift of about 2 nm. The shape of the band on the left side (short-wavelength side) at the half maximum wavelength doesn't change with iron concentration. However, the right side (long-wavelength side) of the peak changes significantly. The position of the half maximum increases significantly with concentration from about 453 to about 466 nm, resulting in a doubling of the FWHM from about 13 nm to 26 nm going from 56.5 ppma to 4730 ppma iron.

The shifting of the long-wavelength half maximum to longer wavelengths (lower energies) with concentration is an indication of the energy per ion reduction as a result of pairing or more complex cluster formation.

Figure 9 shows the normalized spectra as in figure 8, but with eight of the 24 curve-fit samples presented. Note that the half maximum on the short-wavelength side of the peak is nearly constant at 440 ± 0.7 nm. Expanding the region of the graph around the short-wavelength half maximum shows that the spread is not systematic with concentration, but apparently nearly random. Thus, much of the spread is probably a result of slightly different calibrations of the three Hitachi spectrophotometers over several years. The two traces in figure 8 (which represent the Fe³⁺ concentration extremes) were measured on the same instrument by the same operator. The short-wavelength half maximum points are at 439.3 and 440.0 nm, a difference of only 0.7 nm.

The long-wavelength half maximum increases from 453.5 nm at the lowest concentration to 467.2 nm at the highest. With this data on all 24 curve-fit samples, we can plot a curve, shown in figure 10, of the long-wavelength half maximum (left vertical axis) as a function of Fe³⁺ concentration. By taking the short-wavelength half maximum (right vertical axis) as 440 nm, figure 10 also presents the FWHM.

With the quantitative data presented for the amplitude and width of the 450 nm band of Fe³⁺, we can now examine the dependence of the color on the concentration produced by this chromophore. The color produced by most corundum chromophores depends solely on the areal density (ρ_A, in ions per cm²) of the chromophore. The areal density is simply the product of the chromophore concentration (C, in ions per cm³) and the sample’s path length (d, in cm). The areal density is the number of chromophore ions in the sample per cm² as measured by a light beam traversing the sample, as shown in equation 2:

For the chromium chromophore, a sample with 500 ppma Cr³⁺ and a thickness of 1 cm has the same absorbance and color as a sample with 1000 ppma and a thickness of 0.5 cm, because it has the same areal density. The Fe³⁺ chromophore does not share this simple relationship because, as shown in figure 7A, the absorption cross section is not independent of concentration.

In addition to the peak cross section of the 450 nm Fe³⁺ band being dependent on concentration, the band’s FWHM increases with concentration (see figure 10). Thus, the magnitude and shape of the band change with concentration. Since the strength of the Fe³⁺ chromophore depends on both factors, it exhibits a complex dependence on Fe³⁺ concentration. For these reasons, a color calculation for this chromophore requires both the concentration and the sample thickness. The concentration determines the peak cross section and the band shape. A series of band shapes for a range of concentrations is presented in figure 9 and in appendix 1 (https://www.gia.edu/doc/fall-2023-yellow-sapphire-chromophores-appendix1.pdf).

To illustrate these relationships, we present three color circles in figure 11. These three color circles, calculated for a 5000K illumination and a 2° angle of observation, have the same areal density of 665 ppma-cm. For a chromophore such as Cr³⁺, all three color circles would be identical. As we have shown, however, the strength of the Fe³⁺ chromophore increases with the density of Fe³⁺ ions in the sample, even at constant areal density.

Sample 1121 in figure 11 has the highest Fe³⁺ density (4730 ppma) and a strong yellow coloration, even though it is only 0.141 cm thick. The areal density of the sample is 665 ppma-cm. Sample 949 has a lower density at 2960 ppma; to calculate the color, the thickness has been increased to 0.225 cm, producing a matching areal density of 665 ppma-cm. Note that the color saturation is significantly reduced. Finally, sample 1059 has a relatively low iron concentration of 1020 ppma. For the color circle, its thickness has been increased to 0.652 cm to provide a matching areal density of 665 ppma-cm. Again, there is a significant decrease in color saturation. For these reasons, strongly yellow sapphires colored only by iron usually have iron concentrations above 3000 ppma.

As demonstrated above, there is no single curve shape that characterizes the 450 nm Fe³⁺ absorption band. Thus, the effect of iron concentration on the color of ruby or blue sapphire must be calculated separately for each concentration of either Cr³⁺ or Fe²⁺-Ti⁴⁺, and Fe³⁺. The most straightforward calculation would be to simply add in one of the curves presented in appendix 1 to either of the other two chromophores’ spectra for each iron concentration.

The weakest chromophore in natural corundum is Fe³⁺. Yet some very deeply colored yellow sapphires are found in basalt-hosted corundum deposits. These deeply yellow sapphires are colored by the combination of the Fe³⁺ chromophore and the h^•-Fe³⁺ chromophore, and these will be discussed later.

The h^•-Fe³⁺ Chromophore and Heat Treatment.³ Trace elements in the corundum lattice that have a valence less than the 3+ of aluminum are termed acceptors, while those with a valence of greater than 3+ are termed donors (Smyth, 2000). If the sapphire is acceptor dominated, we have the following relationship:⁴

where square brackets indicate concentrations in ppma or ions/cm³. Since solids must be electrically neutral, acceptor excess will be charge compensated by either hydrogen ions, oxygen vacancies (V_o²⁺), or trapped holes (h^•) with a 1+ charge, as shown here:

³As discussed in Dubinsky et al. (2020), h^• will pair with either Cr³⁺ or Fe³⁺. If both are present, it will preferentially pair with Cr³⁺, which lies above Fe³⁺ in the band gap. The absorption spectra of h^•-Cr³⁺ is very different from the h^•-Fe³⁺ spectra, even with the excess Cr³⁺ spectra subtracted out. In this study, we discuss only stones with yellow coloration that contain Fe³⁺ but not Cr³⁺.

⁴Nickel is included in these equations because it was discovered in significant concentrations in various types of natural sapphire by author JS-S. For example, concentrations ranging from 1 to 15 ppma were found in the blue sapphires from Yogo Gulch, Montana. The valence of nickel in natural corundum depends on whether the sum of concentrations of all aliovalent elements results in acceptor or donor domination. Acceptor domination would make nickel 3+, while donor domination would make it 2+. Nickel as a chromophore in corundum will be addressed later in this article.

Whether in nature or in the laboratory, the elimination of the hydrogen ion and/or oxygen vacancies that are a part of the charge compensation of the acceptor excess results in an increase of the trapped hole concentration to maintain charge neutrality. The trapped hole in corundum is an oxygen ion with a charge of –1 rather than the normal –2. The O^1– ion paired with Fe³⁺ is the absorbing specie that creates the yellow coloration, not the divalent ions (figure 12; see also Dubinsky et al., 2020).

While equations 3 and 4 look simple, determining acceptor domination is not. Based on calibrated SIMS measurements at the California Institute of Technology, Division of Geological and Planetary Sciences (Stone-Sundberg et al., 2017, 2020), we have learned that silicon (Si⁴⁺), a donor, is about as common in natural corundum as magnesium (Emmett et al., 2017b). Unfortunately, only a very small portion of the research samples at Crystal Chemistry and in GIA’s colored stone reference collection in Bangkok have been analyzed for silicon by SIMS. The majority of our samples have only been analyzed by quadrupole LA-ICP-MS, which cannot accurately measure silicon in corundum due to close-in-mass interferences, and thus we cannot demonstrate acceptor domination.

Even with measurements for all four trace elements by SIMS, we often cannot determine whether or not a sample is acceptor dominated. This is because the standard deviation (SD) of the acceptor excess is the square root of the sum of the squares of the SDs for the concentrations of each of the four trace elements: magnesium, nickel, titanium, and silicon. Thus, the standard deviation of the acceptor excess can be large and can exceed the value of [h^•] itself, making the determination of acceptor domination impossible. It is also important to note that our chemical analyses are only of several spots on the surface of fabricated wafer samples. We have learned from examination of many heat-treated yellow sapphires that the acceptor domination in a given sample is often spatially nonuniform, and thus our analyses may not have covered the acceptor-dominated region. Spatial nonuniformity in natural corundum is more typical of aliovalent ions than isovalent ions.

This spatial nonuniformity is typical of sapphires from Madagascar, Malawi, and most of the Montana deposits, as well as many of the stones from Sri Lanka. Examples of the nonuniformity of Rock Creek stones are given in Schmetzer and Schwarz (2007) and also shown in figure 13. The yellow region in these stones appears as a smooth spot when viewed down the c-axis. Observed along an a-axis in this figure, it can be seen that the acceptor-dominated region is far more spatially complex.

Figure 14 shows natural yellow sapphires from Sri Lanka colored by this chromophore. The iron concentration in these stones typically ranges from 30 to 250 ppma and is therefore far too small to contribute meaningfully to the coloration as an Fe³⁺ chromophore.

To understand how trapped holes are formed, it is helpful to express the chemical reaction equations in Kröger-Vink notation (see box B). For simplicity, we will assume that the only acceptor is magnesium and that the acceptor excess (Mg^/_excess) is simply written as Mg^/.

BOX B: Kröger-Vink Notation

Defect chemistry is the study of point defects in imperfect crystals. These include vacancies, interstitial atoms or ions, trace elements, electrons, or holes or any other deviation from the structure of a perfect crystal. Even absolutely pure crystals contain point defects at any temperature above absolute zero. The presence of defects is described as “disorder” in a crystal. Modern technological uses of crystalline materials in lasers, semiconductors, lithium batteries, fuel cells, and the like depend on controlled disorder. Allochromatic gems are gems that are colored by impurities. If they were completely pure, they would be colorless. The color of all allochromatic gems is produced by defects. Thus, all color in corundum is caused by defects. Writing the equations for chemical reactions among defects in a crystal is also called defect chemistry. In addition to the normal rules for writing chemical reactions in a liquid or gas, the reactions in a crystal have additional constraints. The set of rules for such reactions is as follows: 1. Mass is conserved: The mass on both sides of a chemical reaction must be equal. 2. Charge is conserved: The bulk of an ideal crystal is electrically neutral. Thus, charged defects must be created or destroyed in combinations that are electrically neutral. Atoms or molecules added to or removed from a crystal must be in electrically neutral combinations. 3. Site balance is conserved: Cation or anion sites can only be created or destroyed in ratios corresponding to the stoichiometry of a perfect crystal. These are also electrically neutral combinations. This is the single most important difference between chemical reactions in a crystal and those in a liquid or gas. The most commonly used formalism for writing chemical reactions with the rules above is the Kröger-Vink notation. The notations are as follows: 1. The main symbol is the species, neutral or ionized, indicated by its usual chemical symbol. Vacancies are denoted by V. The symbol V for vanadium is usually shown in a different font. 2. A subscript indicates a lattice site labeled by its occupant in a perfect crystal. An interstitial site is marked by the subscript i next to a chemical symbol. 3. A superscript indicates the charge of the specie relative to the charge of that site in a perfect crystal. One or more dots (•) are used for extra positive charge(s). One or more slashes (/) are used for extra negative charge(s). An x is used for zero charge difference. Some examples of this notation for corundum are:   Chemical reactions in corundum are written using these symbols. Isovalent ions, which are those ions with the same valence as aluminum or oxygen, can be incorporated as follows:     These equations show metal oxides being incorporated into an aluminum oxide (Al2O3) crystal. No point defects other than the metals themselves are being incorporated, because these trivalent metal ions can have the same valence as aluminum. When corundum crystals are heated in an oxygen atmosphere, oxygen ions take oxygen sites on the surface of the crystal, resulting in the de facto formation of aluminum vacancies on the surface and trapped holes for charge compensation. Oxidation in the bulk of the crystal is by inward diffusion of the resulting aluminum vacancies and holes. The diffusion coefficient of these defects is several orders of magnitude greater than the diffusion of oxygen ions. Therefore, the following equation is a good description of the process:   Aliovalent ions, which have a valence different from that of aluminum or oxygen, can be incorporated into a corundum lattice by the creation of additional defects. For example, charge compensation of divalent ions can be achieved by incorporation of additional oxygen and by the formation of holes as shown here:   In nature, when aliovalent ions are incorporated they are often charge compensated by other aliovalent ions. Here the magnesium is charge compensated by co-incorporation of titanium:   The use of Kröger-Vink notation eliminates several other conceptual reaction possibilities because of the necessity of both charge and site balance. This formalism was proposed in Kröger and Vink (1956) and discussed in even greater detail in Kröger (1974). An excellent reference from which to learn this approach is Smyth (2000).

Acceptor-dominated natural sapphire is often formed in a wet environment. Under these conditions, hydrogen provides the charge compensation, as shown here, and no trapped holes are formed:

However, if the stones are later equilibrated in a warm, dry environment, part or all of the hydrogen may diffuse out of the stones, creating h^•, as shown here:

Since nearly all natural corundum contains significant Fe³⁺, the trapped hole will associate with the Fe³⁺, forming the h^•-Fe³⁺ pair and creating the yellow coloration (see footnote 3). These conditions are common in sapphire from Sri Lanka and the Rock Creek deposit in Montana, where a range of colorless to weakly yellow stones occurs naturally. When the process shown in equation 6 occurs in nature, yellow sapphires are formed, as shown in figure 14.

We usually do not think of hydrogen having a role in the visual color of gem corundum, as we assume the concentrations are very low (Beran and Rossman, 2006), a few ppma at most. Because their absorption cross sections are low (1–2 × 10^–19 cm²), a change of only a few ppma in the valence of the transition metal chromophores will make little or no difference in the apparent color. However, the h^•-Fe³⁺ pair has cross sections of 1–2 × 10^–17 cm², which means that a few ppma change can induce or eliminate intense coloration.

The natural process shown in equation 6 can also be conducted in the laboratory. This is demonstrated in Atikarnsakul and Emmett (2021). If hydrogen-containing acceptor-dominated corundum is heated in an atmosphere that does not contain hydrogen or water vapor, the hydrogen will diffuse out of the stone. For time scales of one hour to several hours and temperatures in the 1000°–1400°C range, hydrogen will be removed from samples whose thickness ranges from a few millimeters to a centimeter.

Diffusion is described by the proportionality in the following equation:

which states that the diffusion distance, x, in cm is directly proportional to the square root of the diffusion coefficient, D, in cm²/sec, multiplied by the time, t, in seconds (Borg and Dienes, 1988).

The diffusion coefficient for hydrogen in aluminum oxide has been studied by many authors (Fowler et al., 1977; Kronenberg et al., 2000; Fukatsu et al., 2003; Belonoshko et al., 2004; Serra et al., 2005; Doremus, 2006; Van Orman and Crispin, 2010), with little agreement in the values they determined. Apparently, the diffusion coefficient is sensitive to impurities or structural issues in the crystal, but that remains to be quantified. For our rough estimates of the time at temperature required to remove the hydrogen from our samples, the hydrogen diffusion coefficient chosen is that given by Belonoshko et al. (2004), which at 1200°C is D = 1.3 × 10^–6 cm²/sec. From this value we can calculate the time required at 1200°C to remove ~90% of the hydrogen from a given size and shape of sample (Shewmon, 1989). For a 2 mm thick sample plate whose lateral dimension is large compared with 2 mm, the time is ~15 minutes. For sample plates that have a lateral dimension that is only a few to several times their thickness, the times would be somewhat less. For larger samples suitable for faceting, the times are significantly longer. For example, removing 90% of the hydrogen from a 1 cm diameter sphere at 1200°C would require heating for approximately 1.5 hours.

From our review of the literature, there is little consensus in the determination of the hydrogen diffusion coefficient in relatively pure sapphire crystals, and no information for natural crystals with the range and variety of trace elements found in gem sapphire. The uncertainty is more than one order of magnitude. According to equation 7, the uncertainty of the time required is then also an order of magnitude. Given the sensitivity of the yellow h^•-Fe³⁺ coloration to hydrogen content, that chromophore might be used as a basis for experiments determining the hydrogen diffusion coefficient in natural or synthetic gem sapphire.

Acceptor domination of weakly colored sapphires from a single deposit ranges from 0 to 90% of the samples: 0% of the samples from Songea in Tanzania, ~20% from Chimwadzulu Hill in Malawi, ~50% from Sri Lanka, and ~90% from Rock Creek in Montana. Thus, it is important to initially test a large lot of small rough to determine the percentage that develop yellow coloration, in order to determine how many wafers must be fabricated to yield a few that turn yellow for the experiments and spectroscopy. This is the approach we have taken for this work, as presented below.

As seen in figure 15 (left), Sri Lankan yellow sapphires were initially a pale yellow color before heat treatment. Figure 15 (right) shows the same samples after heat treatment to quantitatively remove all hydrogen. More than half of the heated stones developed stronger yellow coloration, and many of them show the enhanced color following straight or angular growth structures. Compare the stones in figures 14 and 15. Thus far, it appears that nonuniform coloration is characteristic of this chromophore in natural corundum.

Figure 16 shows the detail of Sri Lankan sample 2802 undergoing this hydrogen removal process. Many natural Sri Lankan sapphires typically display a 3161 cm^–1 OH peak or 3161 cm^–1 OH series in FTIR spectra, which indicates they are acceptor dominated. The connection of the 3161 cm^–1 series with high magnesium content (acceptor domination) was first described by Smith and van der Bogert (2006). Increased yellow coloration after heating (figure 16C) is directly related to the reduction of the amplitude of the OH-related peak at 3161 cm^–1 (figure 16A) (Atikarnsakul and Emmett, 2021) and increased strength of the h^•-Fe³⁺ absorption band in UV-Vis-NIR spectra (figure 16B). Interestingly, the natural characteristic 3161 cm^–1 feature in certain samples could be occasionally transformed to the OH broadband series in the 3000 cm^–1 region with a broadband at 2625 cm^–1, as shown in figure 16A when heated at 900°C in air. When heat treated at 1550°C in pure oxygen, the hydrogen was completely removed, as shown by the disappearance of the OH absorption features from the FTIR spectra. With the removal of the hydrogen, the h^•-Fe³⁺ absorption spectrum and thus the yellow coloration increased.

As mined, sapphire from Rock Creek in Montana has little coloration, which indicates that the acceptor and donor concentrations are quite similar. In addition, about 8% of the stones show some yellow coloration, although only a few would cut a fine yellow gem. We also present hydrogen extraction results for this material, as it shows a different broadband OH absorption spectrum: the wide band 3000 cm^–1 series. Interestingly, a few samples have both the 3000 cm^–1 series and the 3161 cm^–1 series, but thus far none have shown only the 3161 cm^–1 series. When hydrogen is diffused into magnesium-doped synthetic sapphire, the OH spectrum is a broadband at 3000 cm^–1 (Fukatsu et al., 2003). Similarly, when hydrogen is diffused into synthetic sapphire containing Ni³⁺ or Co³⁺, the reduction of these dopants to the divalent state is accompanied by the formation of the broad OH band at 3000 cm^–1 (Müller and Günthard, 1966). These facts, combined with the conversion of the 3161 cm^–1 band to the 3000 cm^–1 band in figure 16A, emphasize how little we understand OH in corundum. It would be worthwhile to study these OH features in a wide variety of acceptor-dominated corundum to determine the correlation of the various OH bands with the trace element chemistry and, perhaps, the formation temperature.

Figure 17 (left) shows run-of-mine samples of Rock Creek sapphire selected only for size (3.0–5.5 mm). Figure 17 (right) shows the same samples after heating for 10 hours at 1200°C in oxygen. Nearly 90% of the stones now show yellow coloration in some portion.

The development of yellow color zones in Rock Creek sapphires is similar to that seen in Sri Lankan sapphire, but the yellow region is often limited to a smaller portion of the stone, as shown in figure 13. Figure 18A shows the FTIR spectra of Rock Creek sample 1021 before and after heat treatment at 1500°C for five hours in pure oxygen. The heat treatment process has fully removed all the hydrogen from the sample.

Figure 18C shows the before and after photos of sample 1021. Heat treatment creates the strongly colored yellow spot that appears in the sample. Note that the optical measurement area is only centered on half of the yellow region (figure 18C, middle). A second sample plate was made so that optical measurements could also be centered on the yellow region, as shown in figure 18C, right.

Figure 18B shows the UV-Vis-NIR spectrum before and after heat treatment and in the second measurement area after heat treatment. The results revealed that the h^•-Fe³⁺ spectrum increased significantly after heat treatment and was more obvious when the analysis area was centered to be exclusively in the yellow area. By subtracting varying amounts of the h^•-Fe³⁺ absorption spectrum from the spectrum in the second measurement area, we can determine that its concentration is approximately 6 ppma, the highest value measured thus far.

Yellow sapphires can also be created by heat treatment of an entirely different type of acceptor-dominated stone that does not contain hydrogen. If acceptor-dominated stones are formed at very low oxygen fugacity, the resulting reaction is:

where the charge compensation is by oxygen vacancies. The result of this reaction is a colorless stone. If such stones are then heat treated at high temperature in an oxygen atmosphere, the oxidation reaction can be described as:

The oxidation is not caused by the inward diffusion of oxygen but by the inward diffusion of aluminum vacancies and holes formed on the surface. The combined reaction (equation 8 plus ½ equation 9) is:

This reaction shows how acceptor-dominated, hydrogen-free colorless stones can be heat treated in oxygen to create the h^•-Fe³⁺ chromophore and thus the yellow coloration. The diffusion coefficient for the inward diffusion of aluminum vacancies and holes is much lower than the outward diffusion of hydrogen, so this reaction requires much higher temperatures and much longer times.

At present we know of three sources for sapphire formed in this way. Pale to colorless stones are found at the Eldorado Bar deposit on the Missouri River in Montana, at the Chimwadzulu Hill deposit in Malawi, and at deposits in Madagascar. In each case, only a fraction (5–30%) of the run-of-mine stones exhibit this chemistry. To study the formation of the h^•-Fe³⁺ chromophore in this entirely different chemistry, the following experiments were conducted. A large 600 g parcel of Missouri River sapphire was processed through a precision splitter to make twelve 50 g test lots that were nearly identical. There were no identifiable yellow samples in the entire 600 g parcel. Twenty-five grams (one-half) of one of the test lots are shown in figure 19A. One each of the 50 g sublots were processed in pure oxygen in each of the following conditions: 1600°C for 10 hours (19B), 1700°C for 10 hours (19C), 1800°C for 10 hours (19D), and 1800°C for 31.6 hours (19E). The experiments at lower temperatures (1200°C and 1400°C) did not produce any yellow stones. After heat treatment, all the yellow sapphires in the 50 g samples were sorted out and photographed separately, as shown in figure 19, B–E.

The stones in figure 19E represent about 23% by weight of the 50 g lot. Plotting the data from these experiments indicates that increasing both the temperature and time should further increase the yield of yellow sapphire and the degree of color saturation.

Comparing the heat treatment conditions of figure 17 (right) and figure 19E shows the dramatic difference between acceptor-dominated stones charge compensated with hydrogen and those charge compensated with oxygen vacancies. Sapphires from Chimwadzulu Hill in Malawi responded to high-temperature heat treatment in a similar way, with about 19% developing the yellow coloration.

If the corundum has excess acceptors and is grown or later equilibrated in a high-oxygen-fugacity natural environment, we have the following chemical reaction:

which is the same as the after-heating result shown in equation 10. The interesting question is whether this condition occurs in nature to produce natural yellow sapphires. To answer this question, we need to find natural yellow sapphires whose coloration is due wholly or in part to the h^•-Fe³⁺ pair yet show no OH absorption features in the FTIR spectrum. Such examples may be found in sapphires that are weakly or strongly yellow colored by Fe³⁺.

Finding such samples is difficult for several reasons. The 3000 cm^–1 broadband usually has a much lower peak absorption coefficient than the 3161 cm^–1 band, as it is much broader. Thus, determining that there is zero OH absorption was difficult, as most of our research samples were rather thin. Additionally, weakly colored yellow sapphires that may also show these two characteristics are not often the focus of sample collection for research, as opposed to more strongly colored stones.

At present, our best example of such a sample is yellow sapphire 4713 from Chanthaburi, Thailand, which shows these two characteristics. As shown in figure 20, there is no indication of the 3161 cm^–1 series or the 3000 cm^–1 broadband series in this FTIR spectrum, but the h^•-Fe³⁺ pair absorption in the UV-Vis-NIR spectrum is clear from the increasing absorption coefficient from 600 to 500 nm. This sample is weakly colored, as it is only 0.465 mm thick. Two small peaks centered at around 2925 and 2852 cm^–1 are observed in the FTIR spectrum, but they are not a part of the 3000 cm^–1 broadband series. They are typically seen overlying various other mid-infrared spectral features as a result of oil contamination on the surface of the stone or other materials present in open fractures. These peaks are related to the C-H stretching (2950–2850 cm^–1) of organic matter (Tanykova et al., 2021), and the peak positions were the same as those of oil-impregnated emerald (Johnson et al., 1999).

Presently, our only example of the equation 11 phenomenon is sample 4713. Definitive proof that natural stones are indeed formed in this way will require the collection of substantially more samples from a wider list of deposits. In addition, samples should be fabricated into significantly thicker wafers to facilitate the accurate measurement of their FTIR spectra.

Combination of the Fe³⁺ and h^•-Fe³⁺ Chromophores. Untreated high-Fe³⁺ yellow sapphires from basalt-hosted deposits such as Australia and Thailand often have a quite uniform yellow color. The color is caused mainly by the Fe³⁺ chromophore, but sometimes it is substantially modified by the presence of the h^•-Fe³⁺ chromophore as well.

Natural yellow sapphires of high iron concentration (>2800 ppma Fe³⁺) usually exhibit a rather uniform yellow coloration. This is because Fe³⁺ is soluble in corundum, easily replacing Al³⁺ because it has the same valence and a similar ionic radius. Unlike the chromophores containing aliovalent ions, Fe³⁺ solubility is not dependent on the presence of another ion. Perhaps more interesting is that these high-Fe³⁺ natural sapphires often incorporate the h^•-Fe³⁺ chromophore as well. It is not unusual to find yellow sapphires colored by Fe³⁺ only and colored by both high Fe³⁺ concentration and the h^•-Fe³⁺ chromophore in the same deposit. The Subera deposit in New South Wales, Australia, and the Khao Ploi Waen/Bang Kha Cha deposit in Thailand are two examples of this phenomenon.

Figures 21 and 22 compare two similar samples from Bang Kha Cha. Sample 941 (figure 21) is colored by Fe³⁺ only, while sample 940 (figure 22) is colored by both chromophores. Both samples exhibit a weak but broad OH band at 3000 cm^–1. Sample 940 has a peak absorption of about 0.04 cm^–1, while sample 941 has a peak absorption of about 0.07 cm^–1.

As discussed earlier, when comparing color caused by the Fe³⁺ chromophore only, both the Fe³⁺ concentration and its areal density must be taken into account. Samples 940 and 941 differ in Fe³⁺ concentration by only 5.1% and in areal density by only 7.1%. Therefore, the 450 nm absorption bands of Fe³⁺ of the two samples are nearly equal. These samples offer a direct comparison of high-iron corundum with and without the h^•-Fe³⁺ chromophore.

The dramatic difference in the depth and character of the color between sample 940 and sample 941 is the result of the additional ~3.2 ppma of the h^•-Fe³⁺ chromophore. When examining the spectra of yellow sapphire samples with high concentrations of Fe³⁺, it is very easy to discern which contain only Fe³⁺ and which contain some addition of the h^•-Fe³⁺ chromo­phore. In figure 21 there is a distinct minimum between the Fe³⁺ 450 nm band and the weak, broad Fe³⁺ band at 530 nm (Borg and Dienes, 1988). Depending on the Fe³⁺ concentration, the minimum between these two usually occurs between 490 and 502 nm. For sample 941, just 0.25 ppma of the h^•-Fe³⁺ pair eliminates the minimum. The 3.2 ppma of the h^•-Fe³⁺ chromophore in sample 940 is determined by subtracting incremental amounts of it from the spectrum of sample 940 until the minimum at 500 nm is restored. Typical concentrations of 1 ppma or more of the h^•-Fe³⁺ chromophore result in a linear increase in the absorption coefficient from 600 to 500 nm, which is very easy to visually recognize. That sample 940 shows a well-saturated color and yet is only 1.43 mm thick attests to the extraordinary strength of the h^•-Fe³⁺ chromophore.

The question naturally arises as to whether these high-iron stones, which also exhibit the h^•-Fe³⁺ chromophore, respond to heat treatment. Figure 23 shows the result of some experiments. Figure 23A gives the FTIR spectra from sample 5270. This natural stone from Australia exhibits the 3000 cm^–1 OH broadband series, not the 3161 cm^–1 series. This OH absorption has been eliminated by heating at 900°C for six hours in air, and then by heating again at 1550°C for six hours in oxygen. Figure 23B illustrates that before heat treatment there is a minimum at ~495 nm, indicating the absence of the h^•-Fe³⁺ chromophore. Heat treatment at 900°C substantially increases the depth of the yellow coloration, as shown in figure 23C.

The combination of high concentrations of both the Fe³⁺ and the h^•-Fe³⁺ chromophores can create dramatic colors, as shown in figure 24.

Beryllium-Diffused Yellow Sapphires. The diffusion of divalent beryllium into natural corundum (Emmett et al., 2003) adds to the concentration of acceptor ions so that equations 3 and 4 become:

The addition of beryllium by diffusion in an oxidizing atmosphere primarily results in the formation of additional trapped holes, which will form more h^•-Fe³⁺ pairs with available Fe³⁺ and thus more yellow coloration. Because beryllium itself is not the chromo­phore, the coloration resulting from trapped holes formed by beryllium excess, by magnesium excess, or by both in excess is the same, as the chromophore is always h^•-Fe³⁺. We have demonstrated this fact by growing two crystals, the first doped with magnesium and iron and the second doped with beryllium and iron.

The E⟂c absorption cross sections of the two h^•-Fe³⁺ chromophores presented in figure 25 are nearly identical. A small vertical offset (0.127 × 10^–17) resulting from internal scatter in the crystal doped with beryllium and iron has been subtracted from its spectrum in figure 25.

Beryllium diffusion to alter the coloration of natural corundum is conducted in an air or pure oxygen atmosphere at temperatures of 1800°C or above for several tens of hours. The diffusion experiments described here were conducted in the Crystal Chemistry laboratory in a pure oxygen atmosphere, as were the experiments in Emmett et al. (2003). Heating in this way eliminates all of the H⁺ and V_o²⁺ charge compensators, maximizing the degree of acceptor domination and the h^•-Fe³⁺ concentration. This maximizes the yellow coloration of sapphire. Commercially this process is often conducted in air. If conducting the diffusion process in air, the water vapor in the air can contribute hydrogen to the process, contributing to some reduction of the h^•-Fe³⁺ concentration. In addition, OH bands that would otherwise have been completely eliminated can appear in the FTIR spectra. This effect in synthetic sapphire is shown in Balmer and Krzemnicki (2015) and Sangsawong (2020).

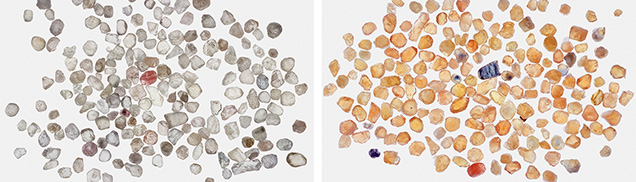
As previously discussed, sapphires that are colorless or weakly colored are usually neutral or slightly acceptor dominated. If such stones are beryllium diffused, a strong yellow color results from a substantial increase in h^•-Fe³⁺ concentration. Figure 26 (left) shows a group of near-colorless sapphires from the Dry Cottonwood Creek deposit in Montana. The great majority of sapphires from this deposit show little coloration. Figure 26 (right) shows the result of beryllium-diffusing this group at 1800°C in oxygen for 33 hours.

The amount of beryllium that can be added to natural corundum by diffusion often quite exceeds the acceptor excess that occurs in natural yellow sapphire. Thus, it is possible that even donor-dominated blue sapphires can be converted to acceptor-dominated yellow sapphires by beryllium diffusion. We conducted an experiment to demonstrate that possibility using deep blue sapphire mined at Kings Plain, New South Wales, Australia (figure 27, left).

Figure 27 (right) shows these stones after beryllium diffusion treatment. The majority of the blues have been converted to yellows, which are now acceptor dominated. Although the color has been reduced in degree, stones that were the deepest blue before diffusion have been lightened but remain donor dominated.

Synthetic Yellow Sapphires. Synthetic yellow sapphire, which is colored by the yellow h^•-Fe³⁺ chromophore, was grown for the first time as a part of the study of the chromophores of natural corundum (Emmett et al., 2017a). The yellow crystal grown by author JS-S at Saint-Gobain Crystal and Detectors was doped with magnesium and iron to produce the h^•-Fe³⁺ chromophore. Figure 28 shows sections of this Czochralski-grown boule, of which the three thickest are 12 mm thick. The other three samples are broken, providing some wedge sections. The h^•-Fe³⁺ chromophore concentration is 2.1 ppma ± 9%. Note the uniformity of color compared to the natural samples colored with the same chromophore, which are often zoned.

Historically, synthetic sapphires have usually been doped with nickel or by nickel and chromium to produce the yellow coloration. The chromophores used have typically been the transition metals and the Fe²⁺-Ti⁴⁺ pair. Thus, it is not surprising to see yellow synthetic sapphire colored primarily with Ni³⁺. It is also interesting that the nickel concentration used is quite low compared with the other transition metals. The yellow coloration from Ni³⁺ does not result from transitions within the Ni³⁺ electronic structure, but from a charge transfer transition from the Al₂O₃ valence band to the Ni³⁺ ion (Tippins, 1970). What is most unusual is that this first charge transfer band of Ni³⁺ peaks is at 400 nm, providing significant absorption from 400 to 480 nm and thus strong yellow coloration. All other transition metals studied to date have their first charge transfer band well into the UV, and thus these bands do not contribute to color. For example, the first charge transfer bands for Fe³⁺ and Cr³⁺ are at 259 and 178 nm, respectively (Tippins, 1970). Charge transfer absorption cross sections are typically a few hundred times stronger than the internal electronic transitions in transition metals, which is why low concentrations of Ni³⁺ contribute significant color.

In the course of this study, we examined one crystal grown with the Verneuil process from RusGems in Bangkok and two crystals grown with the Czochralski technique by Milan Kokta at Saint-Gobain Crystals and Detectors. The Ni³⁺ concentration of the three crystals, analyzed by LA-ICP-MS at GIA and by SIMS at the California Institute of Technology, ranged from 1.6 to 8.0 ppma. To ensure that all the nickel was in the trivalent state, the spectroscopic samples cut from the boules were annealed in oxygen at 1750°C for 10 hours. The oxygen anneal of one of the samples cut from the SS9 Czochralski-grown crystal increased the absorption coefficient of the first charge transfer band by a factor of about eight. This stems from the fact that the oxygen partial pressure of the growth atmosphere is approximately 10^–3 atmospheres, and thus only a portion of the nickel was in the trivalent state following growth. The Verneuil-grown crystal from RusGems was fully oxidized as received. It is unknown whether this condition resulted from the very different growth conditions of the Verneuil process or from an oxygen anneal following growth.

Figure 29 shows sample 1162, cut from Czochralski boule SS9 after the oxygen anneal. Figure 30 shows UV-Vis-NIR absorption cross sections for both E⟂c and Ellc before and after the oxygen anneal. The nickel concentration in this crystal is 3.58 ppma, as measured by SIMS at the California Institute of Technology, and the thickness is 2.14 mm.

As mentioned earlier, the reason for our interest in determining the Ni³⁺ absorption cross section is the fact that nickel in concentrations of up to 15 ppma has been found in natural sapphire. We determined its cross section, as we have done for the other natural chromophores in corundum. As shown here, only a few ppma of Ni³⁺ are necessary to produce substantial coloration. Since the absorption cross section in the visible region of Ni³⁺ exceeds even that of the h^•-Fe³⁺ pair, only a few ppma in a neutral or acceptor-dominated stone would contribute strong absorption in the 400–480 nm region, adding additional yellow coloration. It is important to carefully study the absorption spectra of stones containing ≥1 ppma nickel to determine whether there is a seventh natural chromophore. The first six are discussed in Dubinsky et al. (2020).

CONCLUSIONS

This study of yellow sapphires was motivated by the lack of clarity in the literature as to the origin of the yellow coloration. In retrospect, this uncertainty was the result of three factors. First, the Fe³⁺ concentration in natural stones spans a range of approximately 4–4750 ppma, but only concentrations in the 2000–4750 ppma range contribute significantly to yellow coloration. Second, the h^•-Fe³⁺ chromophore is about 1000 times as strong as the Fe³⁺ chromophore and is often distributed quite inhomogeneously in a given sample. Low concentrations, ≥0.5 ppma, produce substantial coloration, which could only be determined with the advent of LA-ICP-MS and SIMS in gemology. Third, both of these chromophores contribute to the yellow coloration in many natural yellow sapphires, making its cause of color difficult to determine.

We hope this paper will form a basis for further study of the yellow color stability of natural sapphire, a topic that has become increasingly important in recent years. From our work, it is clear that any study of color stability must first determine the trace element composition of the sample down to 1 ppma or better, the UV-Vis-NIR absorption spectra, and the FTIR absorption spectra of the OH ion. A study of color change by low-temperature heating, visible light illumination, or UV illumination will be needed to track the latter two factors.